Thoughts on HO-249
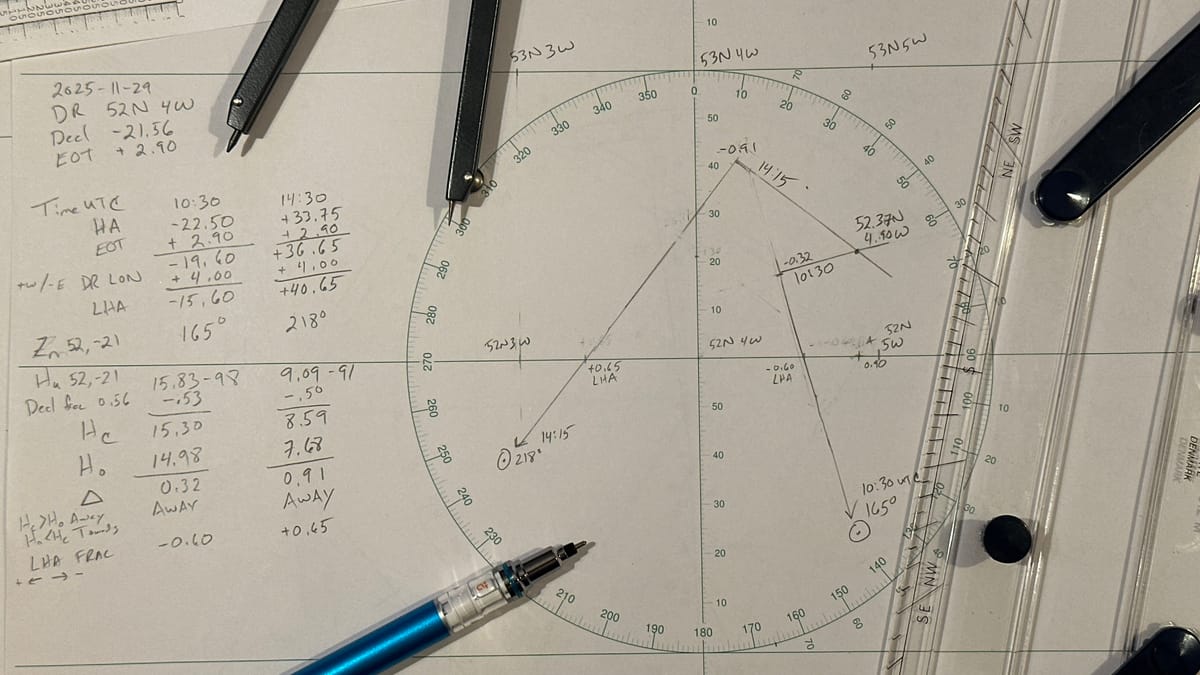
The Nautical Alamanc has free versions of the "Pub. No. 249", a three volume set of sight reduction tables for latitudes up to 89° and declinations up to 29°. Each latitude requires six pages of tables for the 0-180° of local hour angles, so around 270 pages in total.
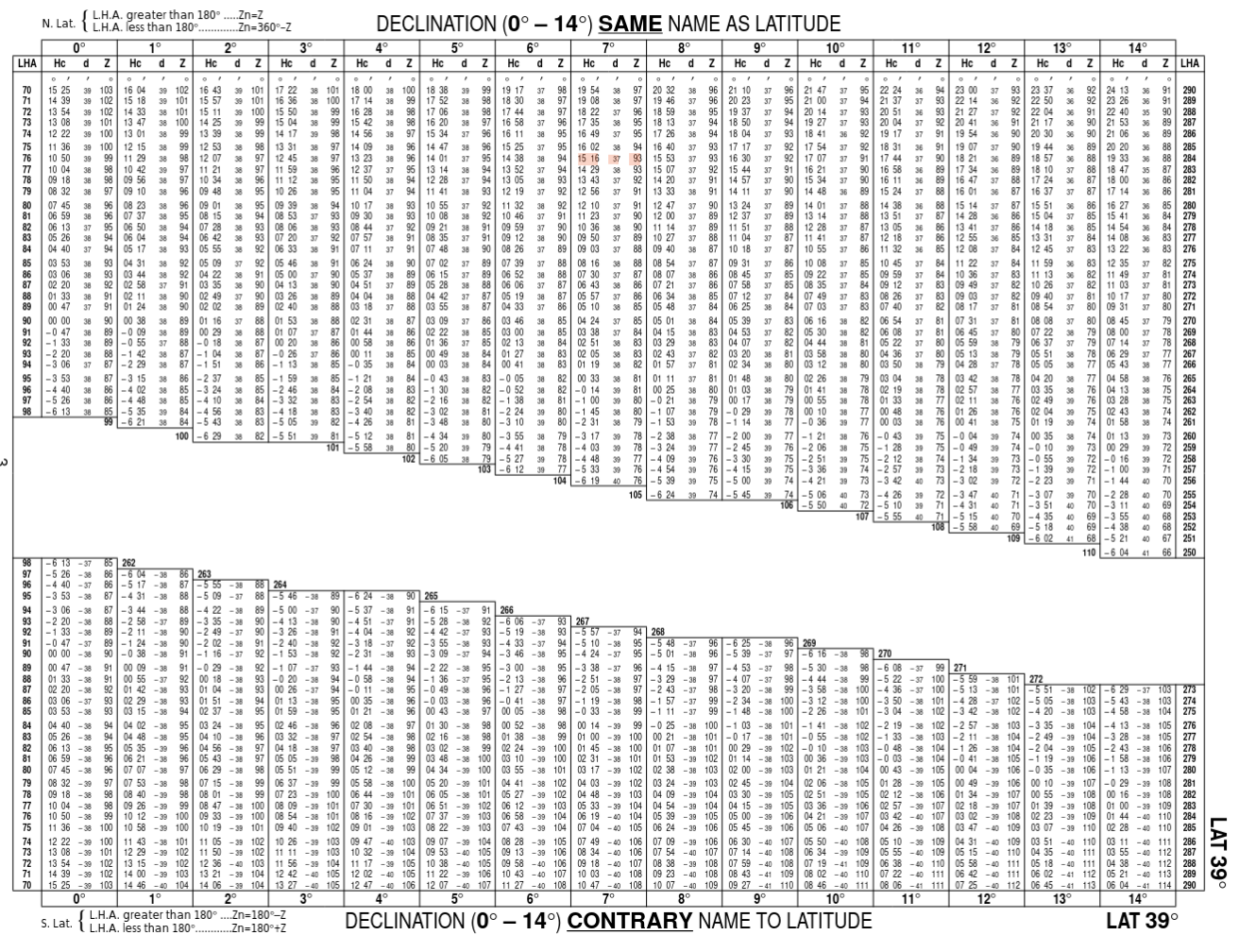
Computing position using the Intercept method requires several lookups and then fixups for the different hemispheres. As an example, for a Local Hour Angle \(LHA\) of +264, you must subtract the \(Z\) value from 180 if you're in the Northern Hemisphere.
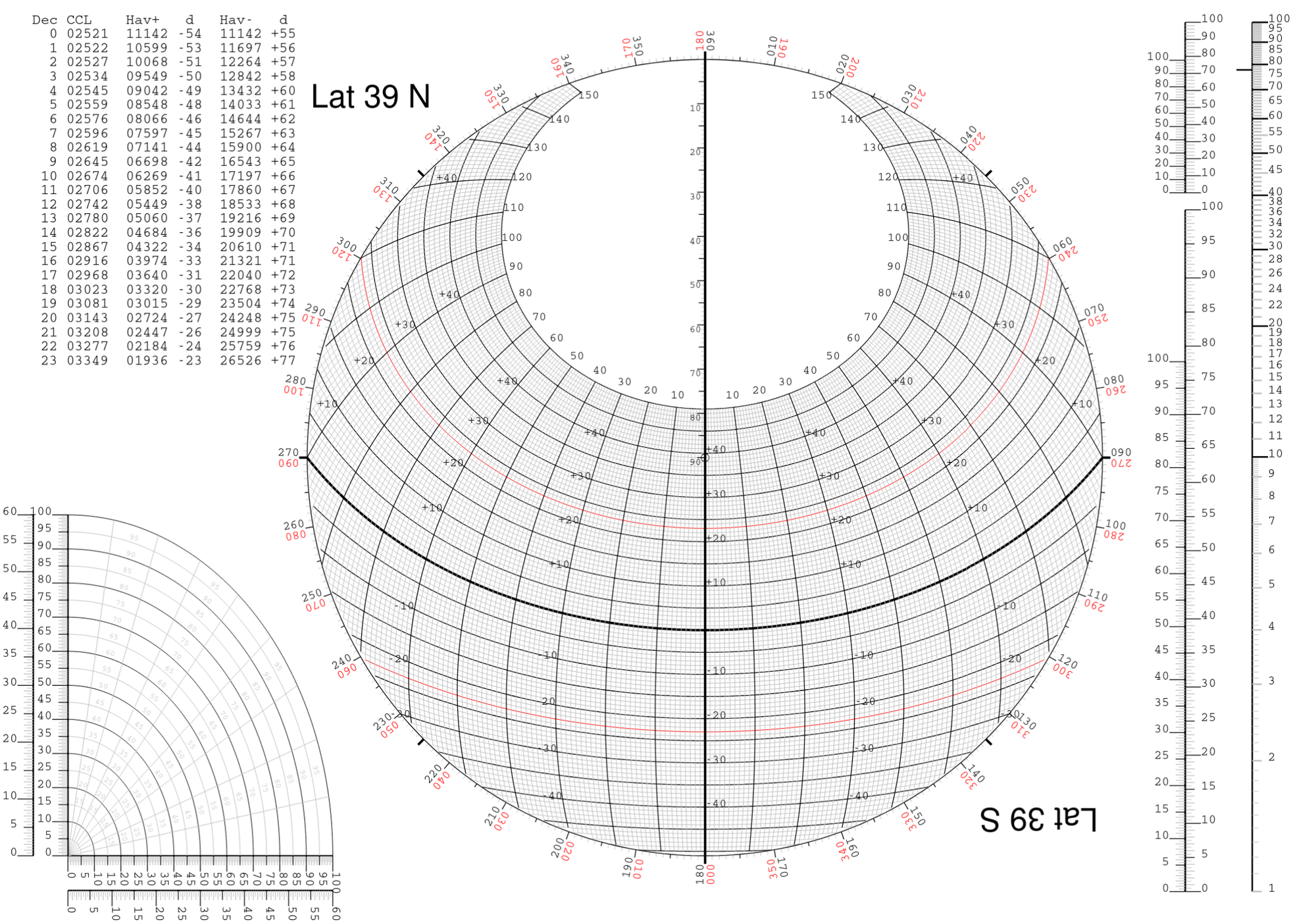
My alternate version of HO249 instead compresses six pages worth of \(Zn\) into a single chart. To find the bearing to an astronomical object you lay a straight edge from the center of the chart to the Local Geographic Position of the star (meaning it's \(LHA\) relative to you and the declination relative to the equator). Continuing the line further gives you a direct reading of the bearing; in the Southern Hemisphere you turn the page upside down and read from the red numbers instead.
This chart also encodes the \(H_c\) values for the Assumed Position \(AP\); you can use a compass or divider to measure the distance from the center to the \(GP\) and then swing it to the scale towards 360 at the top and directly read an approximation of the height of the star. This is not accurate enough for computing the actual intercept, but it lets you know if you're close.
My other complaint is that HO249 pretends that negative numbers don't exist, so there are lots of special cases for "Same Name", "Contrary Name", "Same Name, Declination greater than Latitude", etc. These all go away if you use negative Longitude for East, negative LHA for before local noon and treat north facing Zenith Angles as negative.
What are these values?
The Computed Height \(H_c\) is how high a star is above the ideal horizon for that exact latitude, declination and local hour angle. Note that these are whole numbers, so they are not your exact position, just close enough to it. The difference between your Observed Height \(H_o\) and \(H_c\) is how far away your line of position along the bearing \(Zn\).
If \(H_o > H_c\), then you are close to the star's GP and you should move that many degrees of latitude towards it. If \(H_o < H_c\), then you are further away.
Computing \(H_c\) and \(Z_n\)
These values can also be computed with a calculator or trig table:
$$\sin(H_c) = \sin(Dec)\sin(Lat) + \cos(Lat)\cos(Dec)\cos(LHA)$$
$$\cos(Z) = {\sin(Dec) - \sin(Lat)\sin(H_c) \over \cos(Lat)\cos(H_c)}$$
Or to use the Havesine formula, which avoids bad numeric behaviour at 0 and 1:
$$\hav(90 - H_c) = \hav(LHA)\cos(Lat)\cos(Dec) + \hav(Lat-Dec)$$
$$\hav(Z) = {\cos(Lat-H_c) - \sin(Dec) \over 2\cos(Lat)\cos(H_c)}$$
However, since the bearing only needs to be within a degree, it can be found using the chart with sufficient accuracy.

It might seem that computing \(H_c\) via four multiplications is too much work to do by hand, so there is a way to optimize it and only perform additions. The chart page includes the 23 values for \(CCL=\log(\cos(Lat)\cos(Dec))\) (since \(\cos\) is symmetric around 0 the positive and negative declinations do not matter).
With a trig table that includes both \(\hav(\theta)\) and \(\log(\hav(\theta))\), you can lookup \(\log(\hav(LHA))\) and add it to the CCL value, then look that up in the log part of the table to get the Haversine value, which can be added to the Haversine of the Latitude minus the Declination. These two can be added (they will always be positive) and then that value looked up in the non-log column to get the \(H_c\) value.
I'll expand on this a bit more before my 39c3 talk on Celestial Navigation and hopefully have a custom version of HO249 ready to share.